硅谷sunnyvale

粘滞流体在圆柱形管道中流速随时间演化

在处理粘滞流体在圆柱形管道中的流速随时间变化时，我们需要考虑NavierStokes方程的时间依赖性。这种情况下，通常采用的是一维不可压缩NavierStokes方程，即：

\[ \frac{\partial u}{\partial t} u \frac{\partial u}{\partial x} = \frac{1}{\rho} \frac{\partial p}{\partial x} \nu \frac{\partial^2 u}{\partial x^2} \]

其中：

\( u \) 是流速，

\( t \) 是时间，

\( x \) 是管道的轴向坐标，

\( \rho \) 是流体密度，

\( p \) 是压力，

\( \nu \) 是运动粘度。

这个方程描述了流体在管道中的流动，考虑了压力梯度、粘性以及惯性效应。对于稳态的解析解，我们通常将时间项置为零，即忽略时间依赖性。

然而，《张朝阳的物理课》中提到的是含时方程，这意味着我们需要解决随时间变化的流动问题。一般来说，这需要结合合适的初始条件和边界条件来求解方程。

求解方法

1. 初始和边界条件

我们需要确定初始条件 \( u(x,0) = u_0(x) \)，即初始时刻流速分布。还需要设定管道的边界条件，例如流速在管道两端的固定值或者其他描述流体与管道交互的条件。

2. 数值方法或解析解

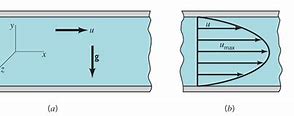
对于一般的含时NavierStokes方程，通常使用数值方法求解。这些方法包括有限差分法、有限体积法或有限元法。数值求解通常需要将空间离散化，并用适当的时间步长进行时间离散化。

3. 解析近似方法

在某些特定情况下，可以使用解析近似方法来获得含时NavierStokes方程的解。这种方法通常基于一些简化假设或者特定的流体行为模型，例如Stokes流体的较低雷诺数情况下的解。

4. 张朝阳的物理课例子

《张朝阳的物理课》可能会展示一些基于数值求解的例子，这些例子通常展示如何利用计算工具（如MATLAB或者Python中的数值库）来求解含时NavierStokes方程。在这些例子中，会详细说明如何设定初始和边界条件，并展示数值解的稳定性和收敛性。

结论

粘滞流体在圆柱形管道中流速随时间的演化是一个复杂的物理问题，需要结合流体力学、数值计算和物理模型来全面理解。在求解过程中，适当的数值方法和合适的边界条件设定对获得可靠的结果至关重要。《张朝阳的物理课》中的例子有助于学习者理解和掌握这些方法，以应对实际工程和科学问题中的挑战。

这些内容希望能为你提供关于粘滞流体在圆柱形管道中流速随时间演化问题的基础理解和求解方法的启发和指导。