去年性价比最高的手机

粘滞流体在圆柱形管中的时间演化特性分析

引言

粘滞流体在管道中的流动特性是流体力学中的一个重要研究领域。特别是在圆柱形管中，流体的速度分布和随时间的演化对于理解和控制流体流动具有重要意义。本文将基于《张朝阳的物理课》中的理论框架，探讨粘滞流体在圆柱形管中的含时方程，分析流速如何随时间演化。

理论背景

在圆柱坐标系中，粘滞流体的运动方程可以表示为纳维斯托克斯方程。对于不可压缩流体，该方程在圆柱坐标系下的形式为：

\[ \rho \left( \frac{\partial \mathbf{v}}{\partial t} \mathbf{v} \cdot \nabla \mathbf{v} \right) = \nabla p \mu \nabla^2 \mathbf{v} \]

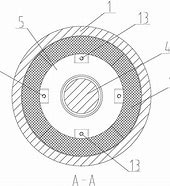
其中，\(\rho\) 是流体密度，\(\mathbf{v}\) 是流体速度矢量，\(p\) 是压力，\(\mu\) 是流体的动力粘度。在圆柱形管中，由于轴对称性，速度矢量可以分解为径向、轴向和周向分量。

初始条件与边界条件

为了求解上述方程，需要设定初始条件和边界条件。初始条件通常设定为流体在管道中的初始速度分布，而边界条件则包括管壁处的无滑移条件，即流体速度在管壁处为零。

含时方程的求解

对于稳态流动，纳维斯托克斯方程可以简化为泊松方程。然而，对于非稳态流动，需要求解含时方程。这通常涉及到数值方法，如有限差分法或有限元法。通过这些方法，可以得到流体速度随时间的变化率，并进一步分析流速的演化过程。

流速的时间演化特性

通过数值模拟，可以观察到粘滞流体在圆柱形管中的速度分布随时间的演化。在初始阶段，由于流体的惯性和粘性力的作用，速度分布会有显著的变化。随着时间的推移，流体逐渐达到稳态，速度分布趋于稳定。这一过程中，流体的粘性力与惯性力的相对作用决定了流速演化的快慢。

结论

粘滞流体在圆柱形管中的流速随时间的演化是一个复杂的过程，涉及到流体的粘性、惯性以及管道的几何形状。通过求解含时方程，可以深入理解这一过程，并为实际应用中的流体控制提供理论基础。

应用前景

了解粘滞流体在圆柱形管中的时间演化特性，对于工程应用如石油输送、化工生产以及生物医学工程等领域具有重要意义。这些知识可以帮助优化管道设计，提高流体输送效率，减少能源消耗。

结语

本文通过分析粘滞流体在圆柱形管中的含时方程，探讨了流速随时间的演化特性。这一研究不仅加深了对流体力学基本理论的理解，也为相关工程技术的发展提供了科学依据。未来，随着计算方法和实验技术的进步，这一领域的研究将更加深入，应用也将更加广泛。