中子星自转角速度的估算

中子星自转角速度的估算可以基于角动量守恒定律和一些观测数据进行计算，下面是一个简单的估算方法：

1. 观测脉冲星的周期

脉冲星是自转速度极快的中子星，它们会定时发出脉冲射电波。通过观测脉冲星的周期，即两次脉冲之间的时间间隔，我们可以初步估算出中子星的自转周期。

2. 应用角动量守恒定律

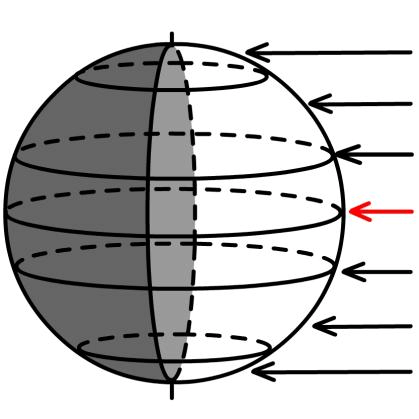
根据角动量守恒定律，中子星的自转角速度可以通过以下公式估算：

\[ L = I\omega \]

其中，\( L \) 为角动量，\( I \) 为中子星的转动惯量，\( \omega \) 为自转角速度。

3. 估算中子星的转动惯量

中子星的转动惯量可以通过一些模型进行估算，如球对称的中子星转动惯量可以表示为：

\[ I = \frac{2}{5}mR^2 \]

其中，\( m \) 为中子星的质量，\( R \) 为中子星的半径。

4. 计算自转角速度

通过观测得到的脉冲星周期以及估算得到的转动惯量，就可以计算出中子星的自转角速度。

在《张朝阳的物理课》中，通过实验和案例展示角动量守恒定律的强大威力可以从多个方面进行：

1. 滑轮和绳子实验

通过滑轮和绳子实验，可以展示当绳子绕过滑轮连接两个物体时，其中一个物体的自转会导致另一个物体的自转，从而呈现出了角动量守恒的现象。

2. 舞者的旋转

以舞者的旋转为例，当舞者双臂向身体收紧自转时，自转速度会加快，这展示了转动惯量的变化和角动量守恒定律的应用。

3. 天体运动的演示

通过模拟天体运动的演示，可以展示天体自转、公转等运动过程中角动量守恒定律的应用，深入理解宇宙中角动量守恒的重要性。

《张朝阳的物理课》通过丰富多彩的案例和实验，生动展示了角动量守恒定律的强大威力，激发学生对物理学的兴趣，并提高他们对自然规律的理解和认识。