android——matrix变换矩阵的探索(1)

如何用矩阵描绘坐标系的变换？

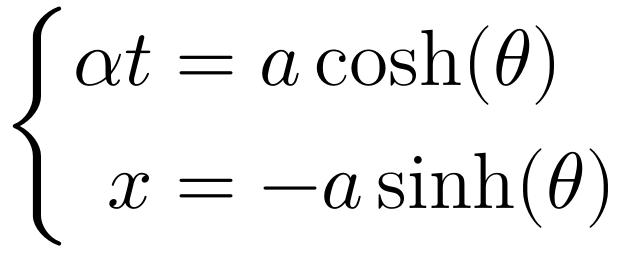
在月中的一个下午，张朝阳的物理课第六十九期开讲，吸引了众多观众在线观看。他首先介绍了一些线性代数的基础概念，用矩阵的方法表示数量的长度，并引出度规的概念；接着寻求出对应的操作矩阵，并验证了直角坐标系在该操作下保持不变；而后他又证明直角坐标系变换到非直角坐标系。

张朝阳首先介绍了线性代数中的一些基本概念，特别是矩阵在表示数量长度方面的应用。他使用矩阵的方法来表示数量的长度，并引出了度规的概念。度规是一个重要的概念，android——matrix变换矩阵的探索(1)它可以帮助我们理解如何在不同的坐标系中测量距离和角度。

接着，张朝阳探讨了如何找到对应的操作矩阵，并验证了直角坐标系在该操作下保持不变。这意味着，无论我们如何旋转或变换坐标系，直角坐标系的性质都不会改变。这是一个非常重要的性质，因为它保证了我们在不同坐标系中的测量结果是一致的。

张朝阳证明了直角坐标系可以变换到非直角坐标系。这是一个更为复杂的过程，因为它涉及到坐标系的非线性变换。然而，通过使用矩阵和度规的概念，我们可以理解这种变换是如何进行的，以及它对我们的测量结果有什么影响。

张朝阳的物理课提供了一个深入理解矩阵和坐标系变换的机会。通过他的讲解，我们可以更好地理解如何在不同的坐标系中进行测量，以及这些测量结果如何相互转换。这对于物理学和其他科学领域的研究都是非常重要的。